MENGUPAS APA ITU FUNGSI INVERS? contoh soal dan pembahasan

FUNGSI INVERS - Fungsi Invers adalah bagian dari fungsi. Materi ini termasuk bagian dari materi SMA. Mari kita bahas mulai dari pengertian, teori, konsep dasar hingga contoh soal.

A. FUNGSI INVERS

Fungsi Invers adalah fungsi dari himpunan A ke B dinyatakan dengan f, maka invers dari fungsi f merupakan sebuah relasi dari himpunan A ke B. Sehingga, fungsi invers dari f : A -> B adalah f^-1: B -> A. dapat disimpulkan bahwa daerah hasil dari f^-1 (x) merupakan daerah asal bagi f(x) begitupun sebaliknya.
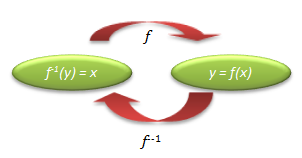
 f^-1 (x) adalah invers dari fungsi f(x). Seperti pada gambar dibawah ini:

Menentukan fungsi invers dengan cara : 

1. Coba misalkan y = f (x)
2. Selesaikan persamaan tersebut untuk menemukan x sehingga diperoleh:
   x = f -1 (y) = g (y)
3. Coba gantilah x dengan y sehingga diperoleh y = f -1 (x) = g (x).
   y = f -1 (x) = g (x) adalah rumus invers untuk fungsi f (x).

         SEHINGGA mengganti f (x)= y = …” menjadi “ f ^-1 (y)= x = …”


Hubungan sifat fungsi invers dengan fungsi komposisi:
1. (f ◦ f^-1)(x)= (f ^-1 ◦ f)(x)= l (x)
2. (f ◦ g)^-1 (x)= (g^-1 ◦ f^-1)(x)
3. (f ◦ g)(x)= h (x)→ f (x)= (h ◦ g ^-1)(x)

untuk memperjelas, silhkan menonton video ini:

Agar lebih paham, marilah berlatih latihan soal dibawah ini: 

NO.1

Tentukan fungsi invers dari f (x) = 3x.

     Pembahasan: 

Misalkan, y = 3x

Selesaikan persamaan tersebut untuk menemukan x = g (y).

Gantilah x dengan y sehingga diperoleh: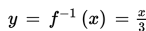

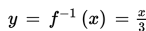
NO.2
 Perhatikan gambar dari diagram panah fungsi f, dengan f : P → Q, berikut.

a. Apakah f -1 ada? Mengapa?

b. Gambarlah diagram panah dari f -1!

c. Carilah (f -1 ○ f)(x), (f -1 ○ f)(y), dan (f -1 ○ f)(z)!

d. Apakah f -1 ○ f = I? Mengapa?

e. Carilah (f ○ f -1)(a), (f ○ f -1)(b), dan (f ○ f -1)(c)!

f. Apakah f ○ f -1 = I? Mengapa?

     Pembahasan

f -1 ada, sebab f berada dalam korespondensi satu-satu.

 Diagram panah dari f -1 ditunjukkan sebagai berikut.

a. (f -1 ○ f)(x) = f -1(f(x)) = f -1(c) = x

b. (f -1 ○ f)(y) = f -1(f(y)) = f -1(a) = y

c. (f -1 ○ f)(z) = f -1(f(z)) = f -1(b) = z

d. Benar bahwa f -1 ○ f = I, sebab (f -1 ○ f)(t) untuk setiap t.

e. (f ○ f -1)(a) = f(f -1(a)) = f(y) = a

     (f ○ f -1)(b) = f(f -1(b)) = f(z) = b

     (f ○ f -1)(c) = f(f -1(c)) = f(x) = c

f. Benar bahwa f ○ f -1 = I, sebab (f ○ f -1)(t) = t untuk setiap t.


APASIH FUNGSI ITU? DAN APASIH FUNGSI KOMPOSISI ITU

Sumber:
1. daniajanto.com
2. yos3prens.wordpress.com
3. matematikadasar.com